Linear Regression and linear transformations:
Alice fits a function \(f(\bx) = \bw^\top\bx\) to a training set of \(N\) datapoints \(\{\bx^{(n)},y^{(n)}\}\) by least squares. The inputs \(\bx\) are \(D\)-dimensional column vectors. You can assume a unique setting of the weights \(\bw\) minimizes the square error on the training set.
Bob has heard that by transforming the inputs \(\bx\) with a vector-valued function \(\bphi\), he can fit an alternative function, \(g(\bx) = \bv^\top\bphi(\bx)\), with the same fitting code. He decides to use a linear transformation \(\bphi(\bx) = A\bx\), where \(A\) is an invertible matrix.
Show that Bob’s procedure will fit the same function as Alice’s original procedure.
NB You don’t have to do any extensive mathematical manipulation. You don’t need a mathematical expression for the least squares weights.
Hint: reason about the sets of functions that Alice and Bob are choosing their functions from. If necessary, more help is in the footnote1.
Answer:
By fitting \(g(\bx) = \bv^\top A\bx\), Bob can only set the function equal to linear combinations of the inputs \((\bv^\top A)\bx = \bw^\top\bx\), where \(\bw = A^\top \bv\). Moreover, just like Alice, all linear combinations are available: any function Alice fits can be matched by setting \(\bv = A^{-\top}\bw\).
As both Alice and Bob are selecting the function that best matches the outputs from the same set of functions, and with the same cost function, they will select the same function.
This form of argument often works for more complex models like neural networks. It would be difficult to generalize a brute-force answer that solves for the fitted function using linear algebra.
Could Bob’s procedure be better than Alice’s if the matrix \(A\) is not invertible?
[If you need a hint, it may help to remind yourself of the discussion involving invertible matrices in the pre-test answers. Also, think about different possible interpretations of “better”.]
Answer:
First we assume \(A\) is square and not invertible, (or rectangular with rank less than \(D\)), then multiple input points (e.g., \(\bx\) and \(\bx'\)) are transformed to the same vector: \(A\bx = A\bx'\). It’s not possible for Bob to assign different function values to two such inputs, whereas Alice can. Bob can no longer fit all the same functions as Alice. Bob can now only choose from some linear combinations of the features \(\bx\), which might not include the combination that minimizes the least-squares cost.
As a result, Bob’s training error might be worse than Alice’s, but can’t be better. However, we don’t usually decide if a model is better based on training error (see w2a), which is one of the most important principles in the course.
If Alice’s fit is well-justified, Bob will also generalize more poorly due to underfitting. However, if \(\bx\) is high-dimensional, or \(N\) is small, Bob’s restricted regression model might avoid overfitting and could generalize better.
There are other ways to consider if Bob’s model might be “better”. For example, for large dimensions \(D\), setting \(A\) to a \(K\ttimes D\) with \(K\!<\!D\) reduces the dimensionality of the data. As well as regularizing the model, this transformation reduces the time and memory required during the least squares fit.
(For completeness: If \(A\) is \(K\ttimes D\) with \(K\!>\!D\), and has rank \(D\), then no information is lost. The matrix is not invertible, but Bob’s set of functions is still the same as Alice, and so he will always get the same fitted function as Alice. There is not a unique way to set the \(K\) parameters \(\bv\) to represent this function however.)
Bonus part: Only do this part this week if you have time. Otherwise review it later.
Alice becomes worried about overfitting, adds a regularizer \(\lambda \bw^\top\bw\) to the least-squares error function, and refits the model. Assuming \(A\) is invertible, can Bob choose a regularizer so that he will still always obtain the same function as Alice?
Answer:
For any model fit \(\bw\) that Alice considers, Bob can set \(\bv = A^{-\top}\bw\) and represent the same function. To penalize every function in the same way as Alice, Bob could substitute \(\bw = A^\top\bv\) into the penalty: \[ \lambda \bw^\top \bw = \lambda \bv^\top A A^\top\bv. \] If we allow this form as a regularizer, then Bob can fit an equivalent model.
If we insist on a regularizer of the form \(\lambda \bv^\top\bv\), then we’d need \(A\) to be (a multiple of) an orthogonal matrix where by definition, \(A A^\top\) is (a multiple of) the identity matrix. Otherwise we don’t see any way to ensure the optimal function is the same.
Bonus part: Only do this part this week if you have time. Otherwise review it later.
Suppose we wish to find the vector \(\bv\) that minimizes the function \[\notag (\by - \Phi\bv)^\top(\by - \Phi\bv) + \bv^\top M \bv. \]Show that \(\bv^\top M \bv = \bv^\top(\frac{1}{2}M + \frac{1}{2}M^\top) \bv\), and hence that we can assume without loss of generality that \(M\) is symmetric.
Why would we usually choose \(M\) to be positive semi-definite in a regularizer, meaning that \(\ba^\top M \ba \ge 0\) for all vectors \(\ba\)?
Assume we can find a factorization \(M = AA^\top\). Can we minimize the function above using a standard routine that can minimize \((\bz-X\bw)^\top(\bz-X\bw)\) with respect to \(\bw\)?
Answer:
This is standard linear algebra manipulation (see background material). Expand out: \[ \bv^\top(\frac{1}{2}M + \frac{1}{2}M^\top) \bv = \frac{1}{2}\bv^\top M\bv + \frac{1}{2}\bv^\top M^\top\bv \] The second term is a scalar, so we can take the transpose of it, and then reorder: \[ = \frac{1}{2}\bv^\top M\bv + \frac{1}{2}(\bv^\top M^\top\bv)^\top = \frac{1}{2}\bv^\top M\bv + \frac{1}{2}\bv^\top M\bv = \bv^\top M\bv. \] As \((\frac{1}{2}M + \frac{1}{2}M^\top)\) is symmetric, and has the same effect as \(M\) in the cost function, we can always choose to specify the cost function with a symmetric matrix.
Usually the purpose of the regularizer is to prevent large weights \(\bv\). If there is a direction \(\ba\) where \(\ba^\top M \ba < 0\) then we can make the second term as negative as we like by making \(\bv\) a large multiple of \(\ba\). Unless the term with \(\Phi\) and \(\by\) prevents it, the minimum cost could be at infinite \(\bv\). The whole point of the regularizer is so we don’t need the data to constrain the parameters however. If we want to guarantee containing the parameters, we should have a strictly positive definite matrix.
For information, we can always obtain the factorization \(M\te AA^\top\). Because we can assume the matrix \(M\) is symmetric, the eigendecomposition of the matrix2 can be manipulated into this form. If the matrix is also positive definite, which it probably should be (why?3), we can use a Cholesky decomposition.
We can then use the same data-augmentation trick as in the lecture notes. Add fictitious observations to the data: \[ \tilde{\by} = \begin{bmatrix}\by\\ \mathbf{0}\end{bmatrix} \quad \tilde{\Phi} = \begin{bmatrix}\Phi\\ A^\top\end{bmatrix}, \] and then set \(\bv\) to minimize \((\tilde{\by}-\tilde{\Phi}\bv)^\top(\tilde{\by}-\tilde{\Phi}\bv)\).
You might have given a different answer based on linearly transforming the data so that the regularizer takes the standard form.
Intended lessons from Q1:
Going forwards, you should immediately recognize that a sequence of linear transformations can be achieved with a single linear transformation. If we want a function to do anything else, we need to introduce non-linearities. However, linear transformations are an important building block, so you need to be able to manipulate and understand them.
Linear transformations, even simple ones such as scaling individual features, do change the effect of a regularization term. Therefore you may need to think about the scale of your data before setting a regularizer (or a grid of \(\lambda\) to explore). Alternatively shift and scale your data so the numbers have zero mean and unit variance. Then default choices for regularizers might work.
Radial Basis Functions (RBFs):
In this question we form a linear regression model for one-dimensional inputs: \(f(x) = \bw^\top\bphi(x;h)\), where \(\bphi(x;h)\) evaluates the input at 101 basis functions. The basis functions \[\notag \phi_k(x) = e^{-(x-c_k)^2/h^2} \] share a common user-specified bandwidth \(h\), while the positions of the centers are set to make the basis functions overlap: \(c_k \te (k-51)h/\sqrt{2}\), with \(k = 1\ldots 101\). The free parameters of the model are the bandwidth \(h\) and weights \(\bw\).
The model is used to fit a dataset with \(N\te70\) observations each with inputs \(x\in[-1,+1]\). Assume each of the observations has outputs \(y\in[-1,+1]\) also. The model is fitted for any particular \(h\) by transforming the inputs using that bandwidth into a feature matrix \(\Phi\), then minimizing the regularized least squares cost: \[\notag C = (\by-\Phi\bw)^\top(\by-\Phi\bw) + 0.1\bw^\top\bw.\]
You’ll want to understand the arrangement of the RBFs to be able to answer this question. Make sure you know how to sketch the situation with pen and paper. However, this second and final core question asks you instead for a straightforward plot using Python.
Write code to plot all of the
K=101basis functions \(\phi_k(x)\) with \(h\te0.2\). Don’t plot data or \(f(x)\) functions.
Answer:
import numpy as np import matplotlib.pyplot as plt def rbf_tut1_q3(xx, kk, hh): """Evaluate RBF number kk with bandwidth hh on input points xx (shape N,)""" c_k = (kk - 51) * hh / np.sqrt(2) return np.exp(-(xx - c_k)**2 / hh**2) # plotting code K = 101 hh = 0.2 xx = np.linspace(-10, 10, 1000) plt.clf() for kk in range(1, K+1): plt.plot(xx, rbf_tut1_q3(xx, kk, hh), '-') plt.show()There is no data to plot here. We asked for the RBFs (plural) rather than one of them or a combined function. When plotting 1D functions, we usually use a dense, evenly-spaced grid. Using a coarse grid or random input points leads to a jagged, unclear plot.
The question asked for a particular function. Answers that change the name or form of the function are harder for others to deal with. Some answers interleaved basis function computation with a complete least squares fitting demonstration. We instead wanted you to have this simple function to help you answer the rest of the question.
There wasn’t one right answer for the x-axis range here. The code above chose a familiar range that would contain the whole region where the RBFs are large. Some of you chose to look at just the range where we’d have data, presumably noticing that most of the RBFs were then not visible.
Explain why many of the weights will be close to zero when \(h\te0.2\), and why even more weights will probably be close to zero when \(h\te1.0\).
Answer:
When \(h\te0.2\) many of the basis functions are several bandwidths away from any of the data’s input locations. These basis functions won’t have any noticeable effect on the function values for \(x\in[-1,+1]\) unless they have huge weights, which is vetoed by the regularization term. As the settings of the weights for these basis function has almost no effect on the first term in the cost function, they will be set close to zero to minimize the second term.
As the bandwidth increases, fewer of the centers are within a few bandwidths of \(x\in[-1,+1]\). More basis functions are given near zero weight.
[The plotting code in a) was intended to get you to look at the arrangement of the basis functions.]
It is suggested that we could choose \(h\) by fitting \(\bw\) for each \(h\) in a grid of values, and pick the \(h\) which led to a fit with the smallest cost \(C\). Explain whether this suggestion is a good idea, or whether you would modify the procedure.
Answer:
Different settings of \(h\) give models that have effectively different numbers of basis functions. While each model has 101 basis functions, many of them will have no effect due to their position and the regularization. It is likely that models with small \(h\), which bring in many active basis functions, will obtain the smallest cost. However, these may not generalize well. Although there is some regularization, making the basis functions narrow, and having more basis functions than data points (\(N\te70\)), is likely to lead to overfitting.
After fitting the weights for each \(h\) on a training set, each model should be evaluated on a validation set to pick the best model.
As we only have \(70\) data points, we might be concerned about having enough data to be able to hold out a validation set. We could consider \(K\)-fold cross validation. Or we might set \(h\) by hand, from experience, to a setting that encourages “reasonable” functions. Or we might try to get more data!
Another data set with inputs \(x\!\in\![-1,+1]\) arrives, but now you notice that all of the observed outputs are larger, \(y\!\in\![1000,1010]\). What problem would we encounter if we performed linear regression as above to this data? How could this problem be fixed?
Answer:
The outputs can only be matched with large function values, which require large weights. The regularization term may cause the fitted function to pass entirely beneath the observed data. We could turn off the regularization, but then we might fit wildly oscillating functions.
One solution is to simply shift and scale the observed \(y\) values to lie within \([-1,+1]\) as before. The predictions would need to be transformed back to the original range.
Another solution is to work with the data at its native scale, but model the offset with a bias term. If we add a new basis function \(\phi_{102}(x) = 1\), the value of the corresponding weight is likely to be around \(w_{102}\approx 1005\). We should not include this parameter in the regularization, or it won’t be able to take on such a large value. Alternatively we could choose \(\phi_{102}(x)\) to be a larger constant.
Intended lessons from Q2:
We can’t fit parameters that control the complexity of a model by minimizing training error, because the most flexible functions always get the lowest training error. We can use cross-validation, although that can be expensive. It is also not necessarily obvious which parameters control model complexity. The Bayesian methods that are covered later in the course are one alternative.
We see that the scale of the data affects what regularization is sensible. Thinking about how to transform the regularization is fiddly, which is why transforming data to lie on a standard scale is so common.
Logistic Sigmoids:
Sketch — with pen and paper — a contour plot of the sigmoidal function \[\notag\phi(\bx) = \sigma(\bv^\top\bx + b),\] for \(\bv \te [1~2]^\top\) and \(b \te 5\), where \(\sigma(a) \te 1/(1\tp\exp(-a))\).
Indicate the precise location of the \(\phi\te 0.5\) contour on your sketch, and give at least a rough indication of some other contours. Also mark the vector \(\bv\) on your diagram, and indicate how its direction is related to the contours.
Hints: What happens to \(\phi\) as \(\bx\) moves orthogonal (perpendicular) to \(\bv\)? What happens to \(\phi\) as \(\bx\) moves parallel to \(\bv\)? To draw the \(\phi\te0.5\) contour, it may help to identify special places where it is easy to show that \(\phi\te0.5\).
Answer:
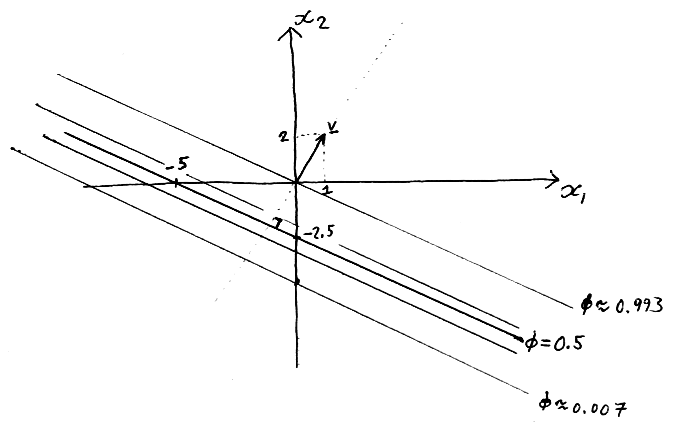
The contours are straight lines, parallel to each other and orthogonal (perpendicular) to \(\bv\). They are symmetrically spaced around the \(\phi\te0.5\) contour, and bunched closer together near that contour.
Any two points where \(\bv^\top\bx + b = 0\) can be used to identify the \(\phi\te0.5\) contour.
If \(\bx\) and \(\bv\) were three-dimensional, what would the contours of \(\phi\) look like, and how would they relate to \(\bv\)? (A sketch is not expected.)
Answer:
The contours of \(\phi\) are now the planes orthogonal (perpendicular) to \(\bv\). These planes are parallel to each other. As before, the function changes most quickly in the direction \(\bv\), and when we are close to the \(\phi\te0.5\) contour plane.
In general, for any number of dimensions, the function is constant within the hyper-planes orthogonal to \(\bv\).
Intended lessons from Q3:
There will be several important explanatory figures in the course, some of them two-dimensional contour plots. So you need to understand contour plots, and not everyone has seen them. The logistic sigmoid function also comes up a lot in machine learning.