A Gaussian classifier:
A training set consists of 14 one-dimensional examples from two classes. The training inputs for the two classes (\(y\te1\) and \(y\te2\)) are:
x1 = [0.5, 0.1, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0.35, 0.25]
x2 = [0.9, 0.8, 0.75, 1.0]In this part you should write code that plots a figure and prints a single number. Please don’t use any libraries except numpy and matplotlib. If you copy the code between your lines of backtics, it should run if you type
%pasteinto a new ipython session.Your code should fit a one-dimensional Gaussian to each class by matching the mean and variance. Then estimate the class probabilities \(\pi_1\) and \(\pi_2\) by matching the observed class fractions. (This procedure fits the model with maximum likelihood: it selects the parameters that give the training data the highest probability.) Then on a single set of axes, plot the scores \(p(x,y) \te P(y)\,p(x\g y)\) for each class
\(y\), as functions of input location \(x\). (This “quick sketch” to help your tutorial discussion doesn’t need labelled axes, or to be beautiful. But please do make good plots for reports, dissertations, etc.)Finally print \(P(y\te1\g x\te0.6)\), the probability that a test point at \(x \te 0.6\) belongs to class 1.
Answer:
This answer does more than was asked to help you check your answers and the later parts as well.
import numpy as np from matplotlib import pyplot as plt x1 = np.array([0.5, 0.1, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0.35, 0.25]) x2 = np.array([0.9, 0.8, 0.75, 1.0]) n1 = x1.size n2 = x2.size pie1 = n1 / (n1 + n2) pie2 = 1 - pie1 mu1 = np.mean(x1) mu2 = np.mean(x2) # These estimates normalize by 1/N var1 = np.var(x1) var2 = np.var(x2) std1 = np.std(x1) std2 = np.std(x2) # These ones use "Bessel's correction" (normalize by N-1). The # variance estimate is now unbiased, but the estimate of std is still # biased (because Jensen's inequality), as are the estimates of # probabilities using the unbiased variance. If N is small enough so # that this difference matters, N-1 isn't going to get rid of your # statistical problems! var1_ub = np.var(x1, ddof=1) var2_ub = np.var(x2, ddof=1) std1_ubv = np.std(x1, ddof=1) std2_ubv = np.std(x2, ddof=1) # x_grid = np.arange(-0.5, 3.5+0.01, 0.01) # alternative x_grid = np.linspace(-0.5, 3.5, 401) def score(x, m, v, pie): return pie * np.exp(-0.5*((x-m)**2)/v) / np.sqrt(2*np.pi*v) test_point = 0.6 score1 = score(test_point, mu1, var1, pie1) score2 = score(test_point, mu2, var2, pie2) p_y1 = score1 / (score1 + score2) print(p_y1) # Version with "unbiased" estimates for the variances: score1 = score(test_point, mu1, var1_ub, pie1) score2 = score(test_point, mu2, var2_ub, pie2) p_y1 = score1 / (score1 + score2) # Plot data and scores for each class: plt.clf() plt.plot(x1, np.zeros(x1.shape), 'bx') plt.plot(x2, np.zeros(x2.shape), 'ro') plt.plot(x_grid, score(x_grid, mu1, var1, pie1), 'b-') plt.plot(x_grid, score(x_grid, mu2, var2, pie2), 'r-') # Quadratic equation from equating scores: # ax^2 + bx + c = 0 # (Solving quadratic equations using the classic formula can have # numerical problems. Use a library routine, or search for how to do # it robustly, if putting something into production that solves many # quadratic equations unattended.) aa = 1/(2*var2) - 1/(2*var1) bb = mu1/var1 - mu2/var2 cc = (np.log(pie1) - 0.5*np.log(var1) - mu1**2/(2*var1)) - \ (np.log(pie2) - 0.5*np.log(var2) - mu2**2/(2*var2)) sol1 = (-bb + np.sqrt(bb**2 - 4*aa*cc)) / (2*aa) sol2 = (-bb - np.sqrt(bb**2 - 4*aa*cc)) / (2*aa) # Show decision boundaries: plt.plot([sol1, sol1], [0, 2.5], 'k-') plt.plot([sol2, sol2], [0, 2.5], 'k-') plt.xlim([-0.5, 3.5]) plt.show()Roughly where on your plot are the “decision boundaries”, the locations where \(P(\text{class 1}\g x) = P(\text{class 2}\g x) = 0.5\)?
You are not required to calculate the locations exactly. You’re aiming to be able to discuss in the tutorial why the decisions change where they do.
Are the decisions that the model makes reasonable for very negative \(x\) and very positive \(x\)? Are there any changes we could consider making to the model if we wanted to change the model’s asymptotic behaviour?
Answer:
The mean of class one is at 0.26, and class two is at 0.86. The standard deviations of the classes are both about 0.1, with class one being slightly wider. The precise estimates you get will depend on whether you used the version containing a normalization of \(N\) or \(N\tm1\). The class 1 curve is higher, despite being slightly broader, because there are more points in class 1.
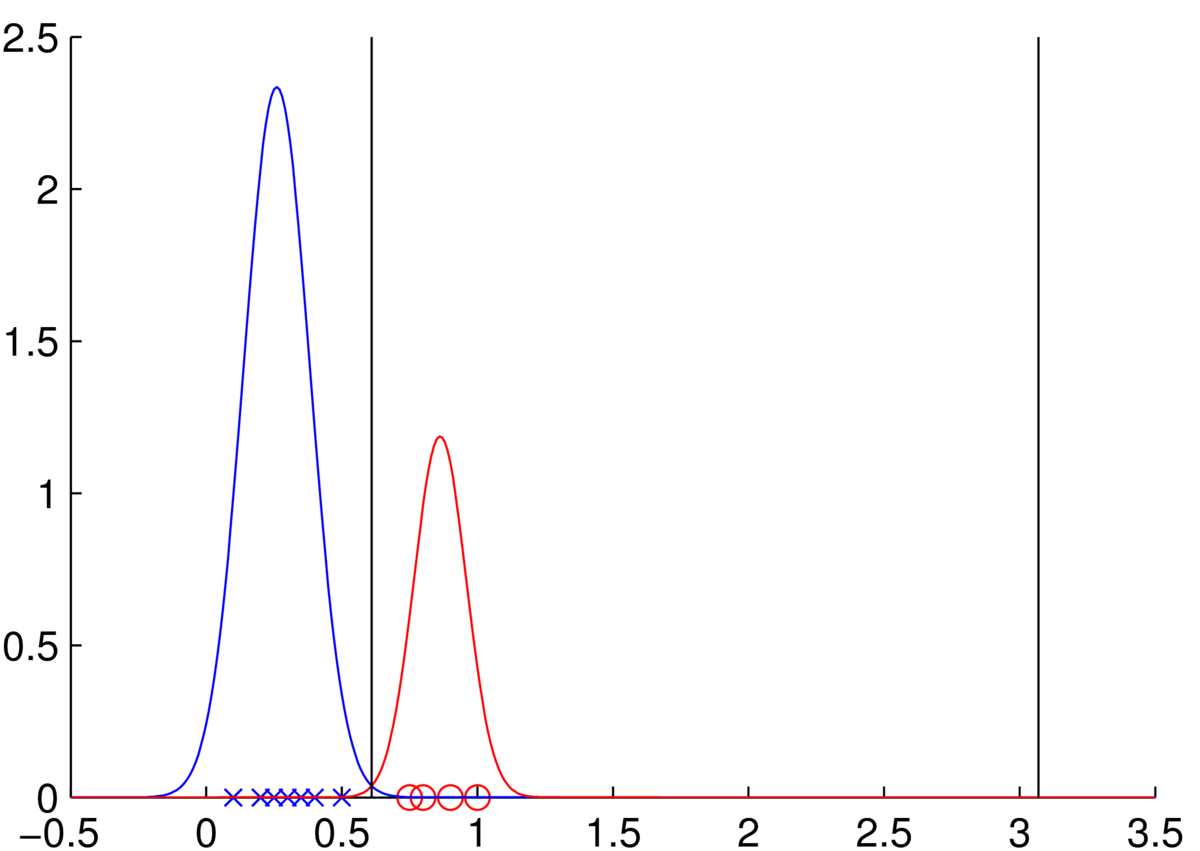
Class 1: blue crosses. Class 2: red circles.
The classification probability is given by Bayes’ rule: \[ P(y\g x) = \frac{p(x\g y)\,P(y)}{\sum_{k=1}^2 p(x\g y\te k)\,P(y\te k)} \]
We set \(P(y\te k) = \pi_k\), given by the empirical class fractions \(\pi_1 = 0.71\) and \(\pi_2 = 0.29\).
We set the class likelihoods to: \(p(x\g y\te k) = \N(x;\,\mu_k, \sigma^2_k)\), with means and variances set to the empirical values.
Substituting that all in we get \(P(y\te1\g x\te0.6) = 0.63\) if we use the “maximum likelihood” estimates of the variances (normalization by \(N\)). However we get \(P(y\te1\g x\te0.6) = 0.52\) if using the unbiased estimates for the variances, using the normalization by \(N\tm1\). Given this small dataset, we favour class 1, but not by much. The model fits are somewhat unreliable.
The diagram shows vertical lines at the decision boundaries where the posterior probabilities for the two classes are equal. To find these locations we equated the scores (prior times likelihood) for the two classes, took logs, and solved the resulting quadratic equation. (You were told you didn’t have to do that. Although you could recognize that there is a quadratic equation and that it might have two solutions, without writing out all the details or solving.)
Because class 2 has lower variance, the tail probability of class 1 eventually becomes bigger than class 2 to the far right of the plot, leading to the second decision boundary. Further to the right, beyond that boundary, we will become incredibly confident that points should be classified as class one. It is hard to justify making confident predictions far away from any of the observed data.
There is no correct answer here. If we changed the tails of the likelihood \(p(x\g y)\), we could change the extreme behaviour. By using a mixture between a uniform and Gaussian, we could make it so that extreme points were given a nearly constant score by each class, leading to nearly uniform predictions. (Although Uniform distributions have to be bounded to be well-defined.)
We might simply give an alert when \(x\) appears far from any observed training input, and refuse to make a classification. How would we decide if \(x\) is “too far”? One idea is to create an extra “outliers” class with a large variance, and assign points to this class along with all of the others.
We might force the class variances to be equal. Then there would be no quadratic term when solving for the class boundary. There would be a single decision boundary, which may or may not be desirable.
Intended lessons: Be able to implement a simple example, so you definitely understand what’s going on. Understand that a broad model can be more probable either side of a more focussed model. Begin to see some problems with fitting simple models to limited data. Be able to discuss alternatives.
Maximum likelihood and logistic regression:
Maximum likelihood logistic regression maximizes the log probability of the labels, \[\notag \sum_n \log P(y^{(n)}\g \bx^{(n)}, \bw), \] with respect to the weights \(\bw\). As usual, \(y^{(n)}\) is a binary label at input location \(\bx^{(n)}\).
The training data is said to be linearly separable if the two classes can be completely separated by a hyperplane. That means we can find a decision boundary \[\notag P(y^{(n)}\te1\g \bx^{(n)}, \bw,b) = \sigma(\bw^\top\bx^{(n)} + b) = 0.5,\qquad \text{where}~\sigma(a) = \frac{1}{1+e^{-a}},\] such that all the \(y\te1\) labels are on one side (with probability greater than 0.5), and all of the \(y\!\ne\!1\) labels are on the other side.
Show that if the training data is linearly separable with a decision hyperplane specified by \(\bw\) and \(b\), the data is also separable with the boundary given by \(\tilde{\bw}\) and \(\tilde{b}\), where \(\tilde{\bw} \te c\bw\) and \(\tilde{b} \te cb\) for any scalar \(c \!>\! 0\).
What consequence does the above result have for maximum likelihood training of logistic regression for linearly separable data?
Answer:
At the decision boundary, \(\bw^\top\bx + b = 0\). Multiplying both sides by \(c\) means \((c\bw)^\top\bx + (cb) = 0\), so scaling the parameters leaves the decision boundary in the same place. We need \(c\!>\!0\) if we want the side of the boundary that corresponds to class 1 to stay the same.
If the data are linearly separable then we can find a decision boundary where every observed label is given probability \(>0.5\). If we leave the decision boundary in the same place, but make the sigmoid steeper by increasing the size of the weights, then the probabilities of the labels under the model will all increase. In the limit \(c\rightarrow\infty\) we confidently (with probability 1) predict all of the labels. We also have no uncertainty at all about predicting any new test point. Is that reasonable?
The costs of some classifiers:
We have a training set of \(N\) examples, with \(D\)-dimensional features and binary labels. This question gets you to revisit what computations you need to do to build and use a classifier.
Assume the following computational complexities: matrix-matrix multiplication \(AB\) costs \(O(LMN)\) for \(L\ttimes M\) and \(M\ttimes N\) matrices \(A\) and \(B\). Inverting an \(N\ttimes N\) matrix \(G\) and/or finding its determinant costs \(O(N^3)\).2
What is the computational complexity of training a generative classifier that models the features of each class by a maximum likelihood Gaussian fit (a Gaussian matching the mean and covariances of the features)?
State your complexity first, then briefly explain how you got it. Include all of the computations that we could reasonably perform based on the training data before seeing the test data, so that test time predictions (part b) will be as cheap as possible.
Answer:
\(O(ND^2 + D^3)\) or \(O(ND^2)\)
But your reasoning was expected; there are right and wrong reasons to dismiss the \(D^3\) term. In an exam, most or even all of the marks might be attached to the explanation rather than an answer.
For your reference we outline all the costs here, but a brief answer might have quickly dismissed the ones that aren’t relevant.
Fitting the class fractions, \(\pi^{(c)}\): \(O(N)\). Sweep through dataset once, maintaining counts for each class.
Fitting all of the class means, \(\{\bmu^{(c)}\}\): \(O(ND)\). Sweep through dataset once, for each example add (D) feature values on to running total for each class.
Fitting the class covariances, \(\{\Sigma^{(c)}\}\): \(O(ND^2)\). Sweep through dataset once, for each of \(N\) examples add \((\bx\tm\bmu^{(c)})(\bx\tm\bmu^{(c)})^\top\) to a running total (cost \(O(D^2)\) per example) for the relevant class. Alternatively (although can have numerical problems) add \(\bx\bx^\top\) within each class and get covariances from these totals and the means. (There are also numerically stable streaming algorithms to compute covariances and means together in a single pass over the data.)
At that point we have the parameters of the model. However, to use the classifier we will need to evaluate expressions involving \(\Sigma^{(c)-1}\) and \(|\Sigma^{(c)}|\) for each class \(c\). We can precompute these terms, or factorizations of \(\Sigma^{(c)}\) from which they can be quickly computed, at training time in \(O(D^3)\) for each class.
You might have correctly said the factorization cost was \(O(KD^3)\) or \(O(CD^3)\) for \(K\) or \(C\) classes. However, the question said we were doing binary classification, so we didn’t need that. There is not a \(K\) or \(C\) in front of the \(O(ND^2)\) cost.
The overall cost is usually dominated by computing the covariances \(O(ND^2)\). We wouldn’t usually include the \(O(ND)\) or \(O(N)\) costs which are asymptotically dominated by that. For large \(D\) the factorization cost could be significant, and people might be interested in the \(D\) scaling, so we included that.
It could be argued that we always want \(N>D\) for the standard Gaussian classifier, because unless we regularized them somehow, the covariances wouldn’t be positive definite. With that reasoning, you might have argued that \(O(ND^2)\) was the only relevant term.
What is the computational complexity of assigning class probabilities to a test feature vector?
Answer:
The log-posterior for each class is: \[ \log P(y\te c\g \bx) = -\frac{1}{2}(\bx-\bmu^{(c)})^\top(\Sigma^{(c)})^{-1}(\bx-\bmu^{(c)}) - \frac{1}{2}\log\big|\Sigma^{(c)}\big| + \log\pi^{(c)} + \text{const.} \] Computing this expression is dominated by \((\Sigma^{(c)})^{-1}(\bx-\bmu^{(c)})\) or an equivalent computation, which is \(O(D^2)\) if the inverse or a factorization of \(\Sigma\) has been precomputed. We compute this score for each class and then the probabilities. [In tutorial 5 Q1 we’ll take a sigmoid (or softmax for \(>2\) classes) to compute the class probabilities neatly.]
You don’t want to redo \(O(D^3)\) matrix factorizations/inversions for each test example. These can be done once at training time.
Bonus parts: If you’re finding the course difficult, leave these for later review:
In linear discriminant analysis we assume the classes just have different means, and share the same covariance matrix. Show that given its parameters \(\theta\), the log likelihood ratio for a binary classifier, \[\notag \log \frac{p(\bx\g y\te1,\,\theta)}{p(\bx\g y\te0,\,\theta)} \;=\; \log p(\bx\g y\te1,\,\theta) - \log p(\bx\g y\te0,\,\theta), \] is a linear function of \(\bx\) (as opposed to quadratic).
Answer:
The expression in the answer to b) is quadratic in \(\bx\) with quadratic term \(-\frac{1}{2}\bx^\top(\Sigma^{(c)})^{-1}\bx\). Taking the difference of two of these terms, the quadratic terms cancel if the class covariances are equal, leaving only terms that are linear or constant with respect to \(\bx\).
When the log likelihood ratio is linear in \(\bx\), the log posterior ratio is also linear. If the log posterior ratio can be written as a linear equation in the form \[\notag \log P(y\te1\g\bx,\theta) - \log P(y\te0\g \bx,\theta) = \bw^\top\bx + b, \] then it can be shown that the predictions have the same form as logistic regression: \[\notag P(y\te1\g\bx,\,\theta) = \sigma(\bw^\top\bx + b), \] but the parameters \(\bw(\theta)\) and \(b(\theta)\) are fitted differently.
How do your answers to a) and b) change when the classes share one covariance? What can you say about the cost of the linear discriminant analysis method compared to logistic regression?
Answer:
At test time the cost is the same as logistic regression: \(O(D)\) to take the inner product of the example with a weight vector.
At training time we still need to compute the shared covariance and to factorize it, which will cost \(O(ND^2 + D^3)\).
(The shared covariance is estimated with the average of \((\bx-\bmu^{(c)})(\bx-\bmu^{(c)})^\top\), using the residual of each datapoint from its class mean.)
Finding the \(\bw\) and \(b\) parameters doesn’t have significant extra cost. Taking the difference between two terms in b) with \(\Sigma^{(1)}\te\Sigma^{(0)}\te\Sigma\) gives a linear term \(\bx^\top\big[\Sigma^{-1}(\bmu^{(1)} - \bmu^{(0)})\big]\). The term in square brackets are the weights \(\bw\), which can be pre-computed in \(O(D^2)\) given a factorization/inverse of \(\Sigma\). Computing the constant terms for the bias is no more expensive.
It is difficult to compare the training cost to logistic regression. Evaluating the log-probabilities for all training items (and gradients) costs \(O(ND)\) with logistic regression. And no \(O(D^2)\) storage is required, so logistic regression scales more easily to enormous numbers of features. For really large datasets, logistic regression training might sweep through the dataset only a few times. For smaller datasets, the iterative optimization procedure can easily cost more in practice than the fixed number of standard matrix computations that linear discriminant analysis requires.
Discussion of Q3:
You should try to get a rough idea of the scaling of algorithms that you learn. We’ve gone into more detail on the book-keeping of costs than we normally would here. However, we think you should be able to see that a Gaussian classifier spends \(O(ND^2)\) time accumulating covariances, and make similar statements for other models. It’s also useful to notice memory costs, here \(O(D^2)\) for each covariance matrix, which can put a hard limit on the scale of problems that can be tackled.
Many machine learning methods are fitted with gradient-based optimizers. It’s common to only consider the cost per update, and assume that only a reasonable number of sweeps through the dataset will be required. Different methods might require different numbers of updates, but that’s often hard to analyse and so ignored.
Computational cost is only one way to compare models. We might also be interested in comparing the accuracy of the models. Linear discriminant analysis makes predictions of the same form as logistic regression. For large datasets, logistic regression is usually more accurate as it explicitly optimizes classification performance using the same family of functions (it’s a “discriminative” rather than “generative” method). However, not setting the class covariances equal creates a non-linear classifier (quadratic discriminant analysis) so a Gaussian classifier can perform better than logistic regression (with no basis functions) when the best decision boundary is non-linear.