Some computation with probabilities: It’s common to compute with log-probabilities to avoid numerical underflow. Quick example: notice that the probability of 2000 coin tosses, \(2^{-2000}\), underflows to zero in Matlab, NumPy, or any package using IEEE 64 bit floating point numbers.
If we have two possible models, \(M_1\) and \(M_2\), for some features, we can define: \[\begin{align} a_1 &= \log P(\bx\g M_1) + \log P(M_1)\\ a_2 &= \log P(\bx\g M_2) + \log P(M_2). \end{align} \] Up to a constant, these ‘activations’ give the log-posterior probabilities that the model generated the features.
Show that we can get the posterior probability of model \(M_1\) neatly with the logistic function: \[ P(M_1\g \bx) = \sigma(a_1 - a_2) = \frac{1}{1 + \exp(-(a_1 - a_2))}. \label{eq:p_m1} \]
Answer:
Bayes’ rule: \(P(M_1\g \bx) = e^{a_1}/Z\) and \(P(M_2\g \bx) = e^{a_2}/Z\), where \(Z = P(\bx)\).
Only two possible models \(\Rightarrow P(M_1\g \bx) + P(M_2\g \bx) = 1, \quad Z = e^{a_1} + e^{a_2}\).
Substituting \(Z\), \[ P(M_1\g \bx) \;=\; \frac{e^{a_1}}{e^{a_1} + e^{a_2}} \;=\; \frac{1}{1 + e^{a_2-a_1}} \;=\; \sigma(a_1 - a_2). \]
Now given \(K\) models, with \(a_k = \log [P(\bx\g M_k)\,P(M_k)]\), show: \[ \log P(M_k\g \bx) = a_k - \log\sum_{k'} \exp a_{k'}. \] The \(\log\sum\exp\) function occurs frequently in the maths for probabilistic models (not just model comparison). Show that: \[ \log\sum_{k'} \exp a_{k'} = \max_k a_k + \log\sum_{k'} \exp \Big(a_{k'} - \max_k a_k\Big). \] Explain why the expression is often implemented this way. (Hint: consider what happens when all the \(a_{k'}\)’s are less than \(-1000\)).
Answer:
With \(K\) models \(P(\bx) = \sum_k P(\bx,M_k) = \sum_k e^{a_k}\), so Bayes’ rule gives: \[ \begin{align} P(M_k\g \bx) &= \frac{e^{a_k}}{\sum_{k'} e^{a_{k'}}}\,, \qquad \text{(a `softmax')}\\ \log P(M_k\g \bx) &= a_k - \log\sum_{k'} e^{a_{k'}}. \end{align} \] This expression involves \(e^{a_k}\)’s. If all the \(a_k\)’s are very negative, these could numerically underflow to zero, we’ll then take the log of zero and obtain
-Inf.We can multiply each of the terms in the sum by \(1 = \exp(b) \exp(-b)\), for any \(b\): \[ \begin{align} \log\sum_{k'} \exp a_{k'} &= \log\Big[\exp(b)\sum_{k'} \exp (a_{k'} - b)\Big]\\ &= b + \log\sum_{k'} \exp (a_{k'} - b). \end{align} \] The expression to be shown set \(b\te \max_k a_k\). In this version, some of the terms might still underflow. However the largest term in the sum is now \(e^0\te1\). Any terms that underflow1 are less than
realmin\(\approx 2\ttimes10^{-308}\), and so even if we had used infinite precision, they would have had no practical effect when added on to a value \(\ge1\).
Pre-processing for Bayesian linear regression and Gaussian processes:
We have a dataset of inputs and outputs \(\{\bx\nth,y\nth\}_{n=1}^N\), describing \(N\) preparations of cells from some lab experiments. The output of interest, \(y\nth\), is the fraction of cells that are alive in preparation \(n\). The first input feature of each preparation indicates whether the cells were created in lab A, B, or C. That is, \(\smash{x_1\nth\!\in\! \{\texttt{A},\texttt{B},\texttt{C}\}}\). The other features are real numbers describing experimental conditions such as temperature and concentrations of chemicals and nutrients.
Describe how you might represent the first input feature and the output when learning a regression model to predict the fraction of alive cells in future preparations from these labs. Explain your reasoning.
Compare using the lab identity as an input to your regression (as you’ve discussed above), with two baseline approaches: i) Ignore the lab feature, treat the data from all labs as if they came from one lab; ii) Split the dataset into three parts one for lab
A, one forB, and one forC. Then train three separate regression models.Discuss both simple linear regression and Gaussian process regression. Is it possible for these models, when given the lab identity as in a), to learn to emulate either or both of the two baselines?
There’s a debate in the lab about how to represent the other input features: log-temperature or temperature, and temperature in Fahrenheit, Celsius or Kelvin? Also whether to use log concentration or concentration as inputs to the regression. Discuss ways in which these issues could be resolved.
Harder: there is a debate between two different representations of the output. Describe how this debate could be resolved.
Answer:
The outputs, being fractions of something, are in the range \([0,1]\). However, the predictions from a Gaussian process regression model, \(p(y_*\g \bx_*, \D)\), are Gaussian distributions, and so predict numbers in \([-\infty,\infty]\). We could consider instead training on and predicting the logit of the fraction of alive cells. The logit is the inverse of the sigmoid function, \(\text{logit}(y) = \log (y/(1-y))\). If all of the fractions are tiny (the vast majority of cells are dead) then the logit is nearly the same as taking the log of the output.
What if sometimes all of the cells are alive, and/or sometimes all of the cells are dead? Then the logit will sometimes return \(\infty\) or \(-\infty\), which we won’t be able to fit. We could consider fitting another function of the outputs, such as \(\text{logit}(0.01 + 0.98y)\). I suspect that, like me, you’ll find this suggestion unsatisfying. It’s become pretty clear that the rescaling is arbitrary.
If many of preparations have all the cells dead (or all alive), I would consider fitting a classifier to predict whether the preparation is either all alive, all dead, or in between. Then I could fit a regression model on the logit of the fraction, for the cases where the fraction isn’t zero or one.
I’d be happier if I could build a more principled model of the data: if we knew the number of cells, as well as the fraction dead, we could model the probability of a cell being alive as the sigmoid of a function. However, we’d then need approximate inference methods (such as the Laplace approximation) to compute the posterior over functions or model parameters. Sometimes fitting a Gaussian model to some scaled data, even if we know it isn’t quite right, is a pragmatic first step.
The lab identity is a categorical variable. A standard way to encode such variables (seen early on in the course) is a 1-of-\(M\), or ‘one-hot’ encoding (also called 1-of-\(K\) and I’m sure other names). The feature is replaced with \(M\te3\) binary features. All but one of the features are set to zero, and one of them is set to one, indicating whether the lab was
A,B, orC. As discussed previously in class, we might use only \(M\te2\) binary features, one forAand one forB, to avoid the inputs being “colinear”.Replacing the lab identity with a single feature in \(\{1,2,3\}\) would not be a good answer in this situation. For linear regression models, this representation gives a model that assumes that, for a given experimental condition, the mean output from lab
Bis always between the mean outputs from labAand labC. We haven’t been given any information that would suggest this assumption is sensible.For more advanced (non-examinable) ways of dealing with multiple related settings you could search for ‘multi-task learning’.
For linear regression: Ignoring the lab feature gives a model with fewer parameters, which is less prone to overfitting if there’s little data. Training three separate models triples the number of parameters; if there’s lots of data it could potentially learn a situation where the three labs lead to completely different linear relationships, although we normally hope that labs will give similar results! Fitting one linear regression model with a one-hot-encoding of the lab adds only three extra parameters. It can emulate the first baseline by setting all of the weights for the lab features to zero. It can’t emulate the second baseline: it can only model a different constant offset to the target function for each lab. Putting the lab into the model as input features could underfit the data if the influence of the labs on the fraction of alive cells depends on the experimental conditions.
For Gaussian process (GP) regression: ignoring the lab feature could still avoid overfitting when there’s little data. If we learn kernel function lengthscales associated with the lab identity features, we can potentially emulate either baseline. Very long lengthscales mean that the lab feature has negligible effect on kernel values, and the lab identity is ignored. Zero lengthscales would mean that the model thinks the functions for the different labs are independent (zero covariance in the Gaussian distributions we construct), so we could train three separate GPs instead. Intermediate lengthscales say that the labs could behave slightly differently, but that the functions for each lab are related, which we’d hope if the experiment is reasonably reproducible!
In some situations, doubling a positive quantity may have a similar-sized effect on the outcome, regardless of the starting value. That is, it’s the log of the quantity that is approximately linearly-related to the output. In these situations taking the log of input features can be necessary to get a good fit with simple linear regression. While GPs can eventually get a close fit to any function, they can require less data to get a good fit if we take the log of an input. Similarly we might need fewer basis functions and/or less data to get a good fit with linear regression with basis functions.
It’s sometimes unclear whether to take logs of positive features however. I would normally take the log of a concentration, but I don’t think I’d usually take the log of a temperature (presumably in Kelvin, so it’s always positive). However, I could be wrong in a particular case, and there will be other features I don’t have good experience with. Therefore, we have multiple possible models, one for each set of feature transformations we want to consider. These could be compared by performance on a validation set, or by marginal likelihood. Alternatively we could create a model with all versions of the features, and hope (perhaps with regularization) we’ll learn some small weights or large lengthscales so that we’ll ignore some of them.
(Warning: models with redundant features can be non-identifiable, and hard to interpret. Without careful regularization they’re more prone to numerical problems and overfitting.)
If we don’t take logs of the temperatures, the units (F, C or K) just set an offset and scaling of the numbers. That will have no effect if we standardize our inputs to have zero mean and unit variance before fitting. Even if we don’t standardize our features, the regression models can learn the same mapping from features to outputs for any offset and scale of the inputs. However, the regularization constants will have different effects for the different scalings of the inputs, which is why we normally standardize our inputs.
Why is comparing transformations of the outputs harder? If we squash the outputs into a narrower range, then the square error or negative log probability we get will go down. That doesn’t mean we are doing better! If different models use different transformations of the output, they need to be converted back to a common scale for comparison. If evaluating probabilistic models of real-valued outputs, densities need to be transformed correctly (using the Jacobian of the transformation). A model is likely to do well on the scale that it was trained to do well on: domain-specific thought is required to decide on which scale we should evaluate a model.
Gaussian processes with non-zero mean:
In the lecture notes we assumed that the prior over any vector of function values was zero mean: \(\bff\sim\N(\mathbf{0}, K)\). We focussed on the covariance or kernel function \(k(\bx\ith, \bx\jth)\), which evaluates the \(K_{ij}\) elements of the covariance matrix (also called the ‘Gram matrix’).
If we know in advance that the distribution of outputs should be centered around some other mean \(\bm\), we could put that into the model by using a Gaussian process prior with mean \(\bm\) such that \(\bff\sim\N(\bm, K)\). Instead, we usually subtract the known mean \(\bm\) from the \(\by\) data, and just use the zero mean model.
Sometimes we don’t really know the mean \(\bm\), but look at the data to estimate it. A fully Bayesian treatment puts a prior on \(\bm\) and, because it’s an unknown, considers all possible values when making predictions. A flexible prior on the mean vector could be another Gaussian process(!). Our model for our noisy observations is now: \[\begin{align} \notag \bm &\sim \N(\mathbf{0}, K_m), \quad \text{$K_m$ from kernel function $k_m$,}\\ \notag \bff &\sim \N(\bm, K_f), \quad \text{$K_f$ from kernel function $k_f$,}\\ \notag \by &\sim \N(\bff, \,\sigma^2_n\mathbb{I}), \quad \text{noisy observations.} \end{align} \] Show that — despite our efforts — the function values \(\bff\) still come from a function drawn from a zero-mean Gaussian process. That is, when \(\bm\) is not observed, the resulting (marginal) distribution of the function values \(\bff\) is a zero-mean Gaussian. Identify the resulting covariance function of the zero-mean process for \(f\).
Identify the mean’s kernel function \(k_m\) for two restricted types of mean: 1) An unknown constant \(m_i \te b\), with \(b\sim\N(0,\sigma_b^2)\). 2) An unknown linear trend: \(m_i \te m(\bx\ith) \te \bw^\top\bx\ith \tp b\), with Gaussian priors \(\bw\sim\N(\mathbf{0},\sigma_w^2\mathbb{I})\), and \(b\sim\N(0,\sigma_b^2)\).
Sketch three typical draws from a GP prior with kernel: \[\notag k(x\ith, x\jth) = 0.1^2\exp\big(-(x\ith-x\jth)^2/2\big) + 1. \] Hints in footnote2.
Answer:
The function \(f\) is the sum of two Gaussian processes. Any vector of values \(\bff\) is the sum of two independent Gaussian vectors: \(\bm\) and a zero-mean draw from \(\N(\mathbf{0}, K_f)\). Thus any set of values are marginally drawn from \(\bff\sim \N(\mathbf{0}, K_m \tp K_f)\), corresponding to a function drawn from a zero mean Gaussian process with covariance function \(k(\bx\ith, \bx\jth) = k_m(\bx\ith, \bx\jth) + k_f(\bx\ith, \bx\jth)\).
What are the statistics of a vector \(\bm\), with identical elements \(m_i \te b\), with ? The vector is Gaussian, and each element has mean zero and marginal variance \(\sigma^2_b\). The other elements of the covariance matrix are given by: \[ \mathrm{cov}[m_i, m_j] = \mathbb{E}[m_i m_j] - \mathbb{E}[m_i] \mathbb{E}[m_j] = \mathbb{E}[b^2] = \sigma^2_b. \] So \(k_m(\bx\ith,\bx\jth) = \sigma^2_b\), and the resulting matrix \(K_m\) has every element set to \(\sigma^2_b\). What we’ve learned: to add a random offset to a process, we can just add a constant to every element of the covariance matrix. (Not just the diagonal: what would that do?)
The covariance function for a linear model is derived in the lecture notes, \(k(\bx\ith,\bx\jth) = \sigma_w^2\bx^{(i)\top}\bx\jth + \sigma_b^2\). If in addition to a random constant offset we want a random linear trend, we further add \(\sigma_w^2\bx^{(i)\top}\bx\jth\) to each element \(K_{ij}\).
A little knowledge is a dangerous thing: Keen students, who actually want to implement Gaussian processes with a linear trend or constant offset, are advised to read Section 2.7, pp27–28, of Rasmussen and Williams, Gaussian Processes for Machine Learning. There can be numerical problems with an obvious implementation using the covariance matrices above.
A final comment: a linear trend is usually physically unrealistic. The model confidently predicts an extreme output if you go to an extreme input location. Under the model, the best way to measure the linear trend is to evaluate the function at extreme input locations. These properties could cause problems if using the model for planning or optimization. It may be better to model a large-scale trend by adding a stationary kernel (such as the squared exponential) with a long lengthscale, rather than the linear kernel.
As referenced in the lecture notes, the GPyTorch toolbox https://gpytorch.ai/ (amongst others) makes it easy to try out different combinations of kernels. See https://docs.gpytorch.ai/en/stable/kernels.html#additivekernel for an example.
The functions you were asked to sketch are from a Gaussian kernel with lengthscale 1 and marginal variance \(0.1^2\), plus a random offset, which has variance 1.
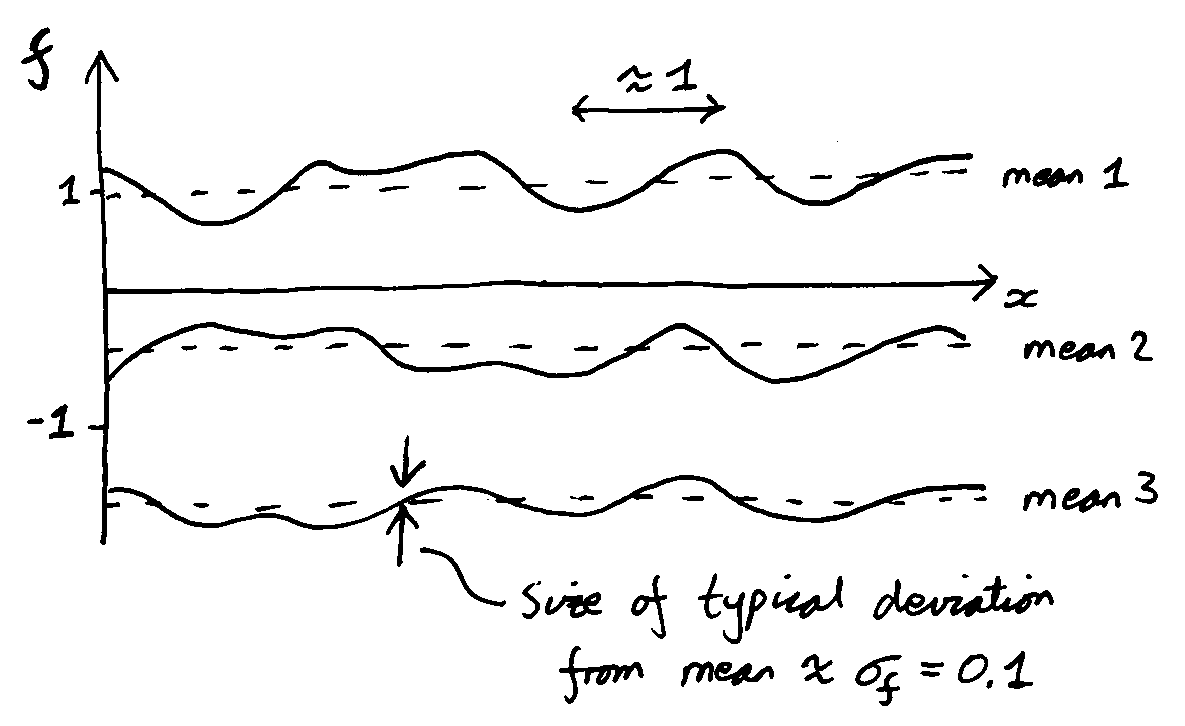
You could plot actual samples on a computer by adjusting the kernel function in the demonstration code provided with the notes. Only a small change to one line is required. If you didn’t get the answer above, you should have checked it, and you should explore the demonstration to help build some understanding.