MLPR revision questions, 2024
Here is a strategy for revising courses: First, go over all the material. You should have already worked on the questions that are raised in the notes. Then for each part, imagine trying to explain it to someone else. Can you say how it relates to other parts of the course? Try to create a small example, application or extreme case and play with it. If you have trouble, find the material in another reference, or ask a friend. If/when you understand the material, imagine what questions could be asked about it. Ask yourself how you might check the answers to those questions yourself.
As a demonstration, we have quickly run over the class materials and, in response to what was there, quickly wrote some further review questions below. They’re less polished and thought out than exam questions, which are designed to have simpler answers. Coming up with questions is something you could also do for yourself, and we encourage you to think beyond what’s here.
As you are moving towards doing independent research or development: you need to be able to come up with questions, and answers, yourself. Therefore, we’re not going to provide detailed worked answers to these questions. However, you could post any queries or your answers on Hypothesis, and give feedback on anyone elses’s answers you see there. We will try to comment on any threads that seem to need it, but there is a deadline: we can’t guarantee any responses in the week before the exam.
Sketch a dataset for binary classification, with two-dimensional inputs \(\bx\), with two tight clusters of points with \(y\te0\) close to \(\bx\te[-5~~{-5}]^\top\) and \(\bx\te[5~~{5}]^\top\), and two tight clusters of points with \(y\te1\) close to \(\bx\te[{-5}~~5]^\top\) and \(\bx\te[5~~{-5}]^\top\).
Write a short Python snippet to generate and plot such a dataset.
Are the two classes linearly separable?
Describe, given only code to do linear least squares regression, how you could fit a classifier to these data with zero training error. (Do not use any other optimizer except the linear regression routine. To check you’re right, you could actually do it…)
What are the pros and cons of replacing linear regression with logistic regression within your method in c)?
Many different classification rules can give zero training error. What makes some better than others? Is there anything you might add to your method in b)/c)?
If we decrease the number of datapoints in the training set, might your code crash at some point? If so, when and why? If not, why not?
In a previous year someone posted a picture on Hypothesis, illustrating how they couldn’t get L2 regularization to work when fitting RBF regression.
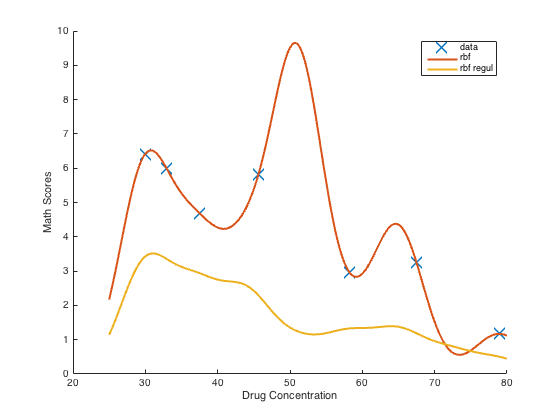
The curve was either too “wiggly”, fitting the training points unreasonably closely, or the weights were forced towards zero too much, and the curve didn’t reach as high as the observed data points. Can you explain what went wrong for them and how to fix it?
A regression dataset of 1000 input-output pairs is split into two parts: 80% for training, 20% for testing. Linear regression is fitted to the data. The sum of square errors on the training set is 788.3, while on the testing set it is 362.2.
Fred says that the examples in the test set must be easier to predict because the test error is much lower. Critique this statement and advise Fred how to monitor performance in future.
Alison says that the model must be overfitting. Why might she say that, and why is it actually not possible to know from the information given?
Ben decides to fit a random forest to the same data. The package has several parameters defining the size of ensembles, the depth of trees, and regularization parameters. He plays around with these, and manages to get a random forest that has a test error of 330.2, which seems “significantly” better than linear regression. State a statistic one might report to give an indication of whether the difference in two test performances means anything. Why is applying a statistical test problematic? What should Ben have done so that it might have been possible to claim that random forests work better for this data source?
The following classification methods are all in active use: \(K\)-nearest neighbours, logistic (or softmax) regression, and neural networks. What are some pros and cons of these approaches that should be considered when choosing a classification method?
Describe a simple iterative algorithm for fitting linear least squares regression. Explain whether your algorithm can set the initial weights to zero, \(\bw\te0\). After someone tries to implement your algorithm, it doesn’t seem to work. What might they do to debug their code?
You are asked to fit a model that can predict a count (a non-negative integer) given a feature vector. You start by developing a standard neural network binary classifier with a sigmoidal output that can predict whether the count is non-zero. You then want to modify the neural network so that the output represents the positive rate of a Poisson distribution. Describe what modifications you would make, including the cost function for training the network, and how this cost can be fitted.
(We didn’t talk about Poisson distributions. But we did talk about modelling data and choosing cost functions based on models. An exam question could ask about distributions we didn’t cover: but it would give you some explanation and any formulae you needed.)A colleague writes code to compute the probability of 10,000 binary labels as predicted by a neural network with a sigmoid output. The code returns zero, and all of the partial derivatives with respect to the weights are also zero, so his learning code terminates immediately. What’s probably gone wrong, and how should your colleague fix it?
You are developing a novel neural network ‘layer’, a function \(f\) with \(K\) free parameters \(\bw\) that transforms an input vector \(\bx\) into a new vector \(\bh = f(\bx; \bw)\). Assume the input \(\bx\) is \(D\)-dimensional and your function costs \(O(D\log D)\) to evaluate. Your code is in a low-level language that runs on a GPU, and the neural network framework that you’re using can’t automatically differentiate it.
Define the inputs and outputs of the function that you need to implement so that the neural network framework can back-propagate derivatives through your layer. What should the big-\(O\) cost of this derivative propagation routine be?
[ Some of you might someday want to implement something nonstandard like: https://arxiv.org/abs/1511.05946 ]Invent a scalar function \(f\) of a matrix \(W\), that uses several matrix-based operations, and derive a matrix-based expression for \(\bar{W}\), where \(\bar{W}_{ij} = \pdd{f}{W_{ij}}\), using the propagation rules in the notes (and/or Giles, 2008).
Given a matrix of students’ course-enrollment data, how might we use machine learning as part of a system to recommend possible alternative courses to a student who has made an initial selection?
What are the things that Bayesian linear regression can do that regularized linear regression can’t, and when might we want to use it?
What is the main difference between a typical Gaussian process model, and a Bayesian linear regression approach with a finite number of basis functions. What are the pros and cons of the GP approach?
Why can the L2 regularization constant not be fitted by minimizing training error. How can a similar constant be fitted without a validation set using a Bayesian approach to linear regression? What additional complications are there for models with non-linearities such as logistic regression or neural networks, and how can they be tackled?
We have seen examples of constrained quantities in this course, positive numbers, numbers in \([0,1]\), positive (semi-)definite matrices. Describe how such constrained quantities can appear in machine learning models and algorithms (think about inputs, outputs, and parameters). Give as many examples as you can of ways we have dealt with such constrained quantities. Where there is more than one option, what are the pros and cons?
I train an auto-encoder on a large collection of varied images. You have a small collection of labelled images for a specialized application. Describe how and why my auto-encoder might be useful in building a classifier for your application.
If you wanted to make an autoencoder to model binary feature vectors, are there any design choices you might consider changing compared to a generic autoencoder for real-valued data?
One way to stop the weights for logistic regression growing large is to add an L2 penalty \(\lambda\bw^\top\bw\) and pick the \(\lambda\) that gives the fit that gives the best validation performance. Describe another method that we’ve covered in this course to control the scale of the weights, that does not require a validation set, but instead is able to decide how much to limit the size of the weights based on the training data.
Someone told us that they’d reimplemented the neural network from assignment 2 in TensorFlow using a stochastic gradient optimizer, but it worked less well. Why are stochastic gradient methods so popular compared to second-order batch methods, when they can be harder to tune and get to converge?
… these questions don’t cover everything in the course. You will be asked new questions that aren’t here, in the notes, or in past papers. The most important thing is to understand the basic machine learning methods and how to set them up. There’s no point knowing the more advanced material, without that solid foundation, and the foundations are examined the most heavily. Getting a high mark will require having some grasp of everything, and some ability to use the maths in the notes.